我们在谈论什么与伽罗瓦有关的东西?
在我们深入加密的世界之前,让我们先来了解一下伽罗瓦域到底是什么。伽罗瓦域以年轻的法国数学家埃瓦里斯特·伽罗瓦命名(有趣的是,他在20岁时因决斗而去世——真是轰轰烈烈地离开了这个世界)。这些域是具有特殊代数性质的有限元素集合。
简单来说,想象一个数字的游乐场,这里的数字遵循非常特定的规则。这些规则确保无论你如何加、减、乘或除这些数字(除以零除外,因为即使在数学中,我们也不能除以零),你总是会得到游乐场中的另一个数字。
加密连接:为什么伽罗瓦域很重要
现在,你可能会想,“这故事挺酷的,但这和保护我的猫咪表情包有什么关系?”好问题!伽罗瓦域是一些不太知名但日益重要的加密系统的基础。以下是它们引起轰动的原因:
- 效率:在伽罗瓦域中的运算可以非常快速和高效,这对于实时加密至关重要。
- 抗攻击性:它们对某些类型的加密攻击提供了强大的抵抗力。
- 灵活性:不同大小的伽罗瓦域可以用于创建不同级别的安全性,使其适应不同的需求。
伽罗瓦域的实际应用:现实世界中的加密系统
让我们看看一些正在使用伽罗瓦域的加密系统:
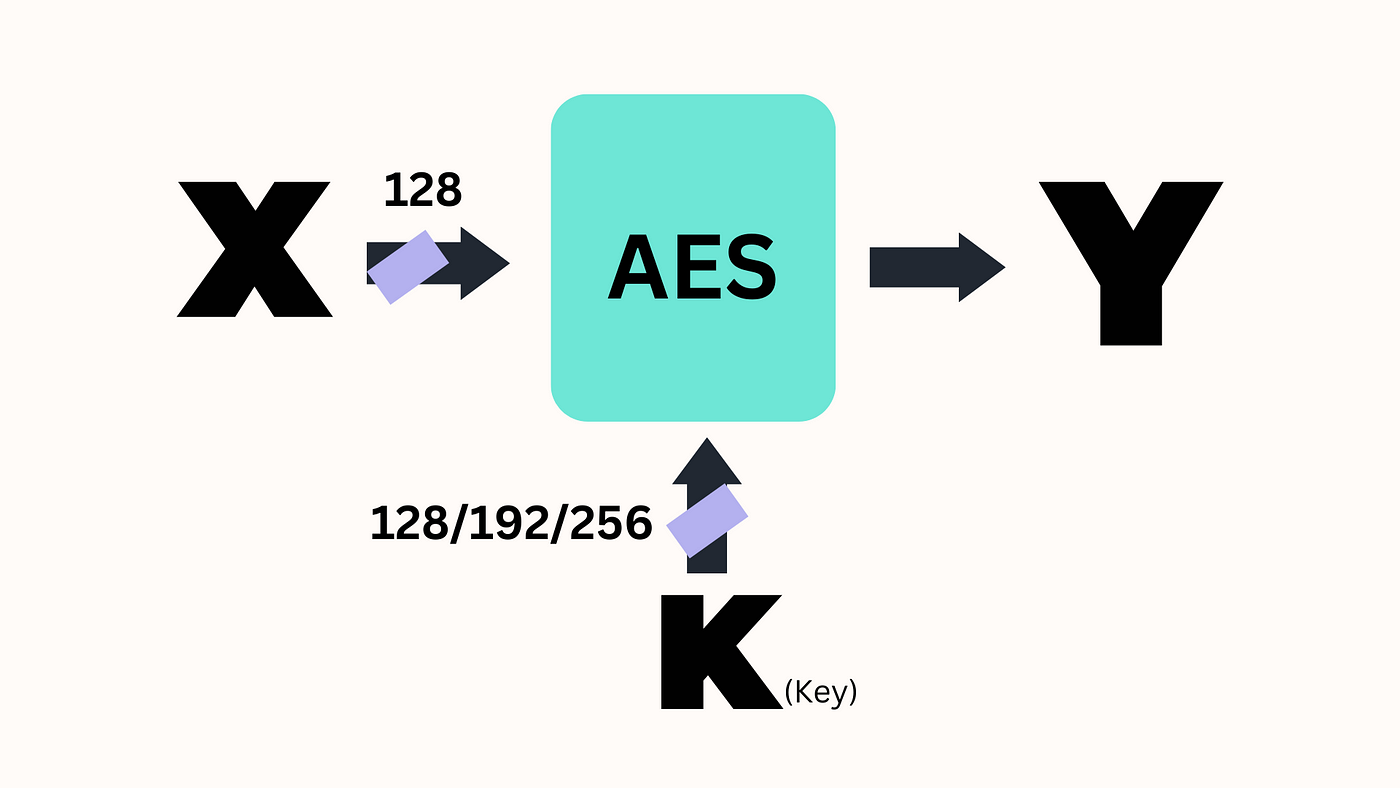
1. 高级加密标准(AES)
是的,就是那个AES。虽然不算“下一代”,但AES在其MixColumns步骤中使用了伽罗瓦域GF(2^8)的运算。这有助于创建安全加密所需的混淆和扩散。
2. 里德-所罗门纠错
虽然主要用于数据传输和存储中的纠错,但基于伽罗瓦域算术的里德-所罗门码在加密中也有应用,特别是在秘密共享方案中。
3. 椭圆曲线加密(ECC)
ECC在有限域上运行,通常是伽罗瓦域。这使得在保持相同安全级别的同时,可以使用比RSA更小的密钥。
下一个前沿:后量子加密
这里是事情变得真正有趣的地方。随着量子计算机的出现,威胁到我们当前的许多加密方法,加密专家正在转向伽罗瓦域来开发抗量子算法。
基于代码的加密
一个有前途的领域是基于代码的加密,它在很大程度上依赖于伽罗瓦域中的运算。例如,McEliece加密系统使用有限域上的纠错码来创建一个被认为是抗量子的公钥加密系统。
以下是伽罗瓦域在基于代码的加密中可能使用的一个简化示例:
import galois
# 创建一个大小为2^8的伽罗瓦域
GF = galois.GF(2**8)
# 生成一个随机消息
message = GF.Random(10)
# 生成一个随机错误向量
error = GF.Random(10)
# 模拟编码和添加错误
encoded_message = message + error
# 实际上,解码将涉及使用伽罗瓦域性质的复杂算法
decoded_message = encoded_message - error
print(f"原始消息: {message}")
print(f"解码消息: {decoded_message}")
print(f"它们相等吗? {all(message == decoded_message)}")
当然,这是一个非常简化的示例。真正的基于代码的加密系统涉及更复杂的操作和更大的域大小。
挑战和考虑
在你准备用伽罗瓦域重写所有加密代码之前,让我们考虑一些挑战:
- 复杂性:使用伽罗瓦域需要对抽象代数有扎实的理解。这不是心脏脆弱(或数学不好)的人能轻易掌握的。
- 实现:在硬件上高效实现伽罗瓦域算术可能很棘手,尤其是在未针对这些操作进行优化的硬件上。
- 标准化:许多基于伽罗瓦域的加密系统仍处于研究阶段,尚未广泛标准化。
那么,为什么这么重要?
伽罗瓦域不仅仅是一个数学上的好奇心。它们为新一代加密系统提供了基础,这些系统承诺更快、更高效,并可能抗量子攻击。随着我们进入一个数据安全比以往任何时候都更为重要的时代,这些数学结构可能在保护我们的数字生活中扮演越来越重要的角色。
无论你是加密爱好者、安全专业人士,还是只是想在聚会上显得聪明的人,了解伽罗瓦域在现代加密中的作用绝对值得你花时间。谁知道呢?数据安全的下一个突破可能正来自这些有限的无限可能性域。
“做数学的艺术在于找到包含所有普遍性萌芽的特殊情况。” - 大卫·希尔伯特
在现代加密的情况下,这个特殊情况可能正是伽罗瓦域。所以下次有人问你关于加密的未来时,你可以自信地说:“一切都与伽罗瓦有关,没问题。”
进一步阅读
如果你对此感兴趣并想深入了解伽罗瓦域及其在加密中的应用,以下是一些资源供你开始:
记住,在加密的世界中,今天的前沿就是明天的过时。保持好奇,继续学习,谁知道呢?也许你就是下一个在加密领域发现重大突破的人。愿伽罗瓦与你同在!